问题
解答题
| 已知抛物线C1:y=ax2+4ax+4a-5的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1. (1)求抛物线的解析式和顶点P的坐标; (2)将抛物线沿x轴翻折,再向右平移,平移后的抛物线C2的顶点为M,当点P、M关于点B成中心对称时,求平移后的抛物线C2的解析式; (3)直线y=-
|
答案
(1)由抛物线C1:y=ax2+4ax+4a-5=a(x+2)2-5得
∴顶点P的坐标为(-2,-5)
∵点B(1,0)在抛物线C1上,∴a=5 9
∴抛物线C1的解析式为y=
x2+5 9
x-20 9
;25 9
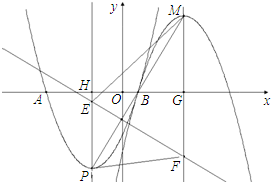
(2)连接PM,作PH⊥x轴于H,作MG⊥x轴于G
∵点P、M关于点B成中心对称
∴PM过点B,且PB=MB
∴△PBH≌△MBG
∴MG=PH=5,BG=BH=3
∴顶点M的坐标为(4,5)
∴抛物线C2的表达式为y=-
(x-4)2+5;5 9
(3)依题意得,E(-2,
+m),F(4,-6 5
+m),HG=612 5
①当E点的纵坐标小于-5时,
PE=-5-(
+m)=-6 5
-m,MF=5-(-31 5
+m)=12 5
-m,37 5
∴s=
(-1 2
-m+31 5
-m)×6=-6m+37 5
;18 5
②当E点的纵坐标大于-5且F点的纵坐标小于5时,
PE=
+m-(-5)=6 5
+m,MF=5-(-31 5
+m)=12 5
-m,37 5
∴s=
;204 5
③当F点的纵坐标大于5时,
PE=
+m-(-5)=6 5
+m,MF=-31 5
+m-5=-12 5
+m37 5
∴s=6m-
.18 5