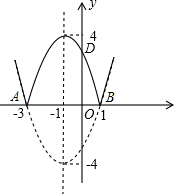问题
解答题
| 已知二次函数y=x2-2mx+m2-4的图象与x轴交于A、B两点(点A在点B的左边),且与y轴交于点D. (1)当点D在y轴正半轴时,是否存在实数m,使得△BOD为等腰三角形?若存在,求出m的值;若不存在,请说明理由; (2)当m=-1时,将函数y=x2-2mx+m2-4的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象Ω.当直线y=
|
答案
令y=0得x2-2mx+m2-4=0,解得x1=m-2,x2=m+2,
∴A(m-2,0),B(m+2,0),D(0,m2-4),
(1)∵点D在y轴正半轴,
∴m2-4>0,设存在实数m,使得△BOD为等腰三角形,则BO=OD,
即|m+2|=m2-4,
①当m+2>0时,m2-4=m+2,解得m=3或m=-2(舍去);
②当m+2<0时,m2-4+m+2=0,解得m=1或m=-2(都舍去);
③当m+2=0时,点O、B、D重合,不合题意,舍去;
综上所述,m=3.
(2)当m=-1时,y=x2+2x-3,则A(-3,0),B(1,0)顶点为(-1,-4)
因为直线y=
x+b与图象Ω有两个公共点,1 2
则当直线y=
x+b过A点时b=1 2
,3 2
当直线y=
x+b过B(1,0)时,b=-1 2
,1 2
当直线y=
x+b与y=-x2-2x+3只有一个公共点时,b=1 2
,73 16
根据图象,可得-
<b<1 2
或b>3 2
.73 16