问题
解答题
数列{an}满足Sn=2n-an(n∈N*).
(1)计算a1,a2,a3,a4,并由此猜想通项公式an;
(2)用数学归纳法证明(1)中的猜想.
答案
(1)a1=1,a2=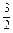 a3=
a3=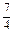 a4=
a4=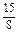 an=
an=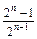 (n∈N*)(2)证明略
(n∈N*)(2)证明略
(1)解 当n=1时,a1=S1=2-a1,∴a1=1.
当n=2时,a1+a2=S2=2×2-a2,∴a2=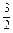 .
.
当n=3时,a1+a2+a3=S3=2×3-a3,∴a3=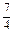 .
.
当n=4时,a1+a2+a3+a4=S4=2×4-a4,∴a4=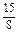 .
.
由此猜想an=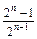 (n∈N*).
(n∈N*).
(2)证明 ①当n=1时,a1=1,结论成立.
②假设n=k(k≥1且k∈N*)时,结论成立,即ak=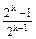 ,
,
那么n=k+1时,
ak+1=Sk+1-Sk=2(k+1)-ak+1-2k+ak=2+ak-ak+1.
∴2ak+1=2+ak,
∴ak+1=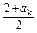 =
=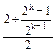 =
=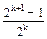 ,
,
这表明n=k+1时,结论成立,
由①②知猜想an=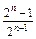 (n∈N*)成立.
(n∈N*)成立.
