问题
解答题
甲、乙二人进行一次围棋比赛，约定先胜3局者获得这次比赛的胜利，比赛结束．假设在一局中，甲获胜的概率为0.6，乙获胜的概率为0.4，各局比赛结果相互独立．已知前2局中，甲、乙各胜1局，
(Ⅰ)求甲获得这次比赛胜利的概率；
(Ⅱ)设ξ表示从第3局开始到比赛结束所进行的局数，求ξ的分布列及数学期望。
答案
解：记Ai表示事件：第i局甲获胜，i=3，4，5，
Bj表示事件：第j局乙获胜，j=3，4，
(Ⅰ)记B表示事件：甲获得这次比赛的胜利，
因前两局中，甲、乙各胜一局，故甲获得这次比赛的胜利当且仅当在后面的比赛中，甲先胜2局，
从而B=A3·A4+B3·A4·A5+A3·B4·A5，
由于各局比赛结果相互独立，故
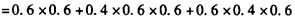=0.648；
(Ⅱ)ξ的可能取值为2，3，
由于各局比赛结果相互独立，
所以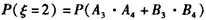
，
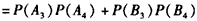
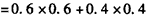
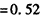P(ξ=3)=1-P(ξ=2)=1-0.52=0.48，
ξ的分布列为
ξ | 2 | 3 |
P | 0.52 | 0.48 |
。
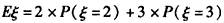
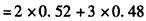
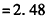