问题
解答题
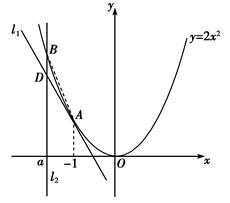
如右图所示,已知A为抛物线C:y=2x2上的点,直线l1过点A,且
与抛物线C相切,直线l2:x=a交抛物线C于点B,交直线l1于点D.
(1)求直线l1的方程;
(2)求△ABD的面积S1.
答案
(1)由条件知点A为直线l1与抛物线C的切点,
∵y′=4x,∴直线l1的斜率k=-4,
即直线l1的方程为y-2=-4(x+1), 即4x+y+2=0.
(2)点A的坐标为(-1,2),
由条件可求得点B的坐标为(a,2a2),
点D的坐标为(a,-4a-2),∴△ABD的面积S1为
S1=×|2a2-(-4a-2)|×|-1-a|
=|(a+1)3|=-(a+1)3.
