问题
解答题
抛物线y=mx2+(m-3)x-3(m>0)与x轴交于A、B两点,且点A在点B的左侧,与y轴交于点C,OB=OC.
(1)求这条抛物线的解析式;
(2)若点P(x1,b)与点Q(x2,b)在(1)中的抛物线上,且x1<x2,PQ=n.
①求4x12-2x2n+6n+3的值;
②将抛物线在PQ下方的部分沿PQ翻折,抛物线的其它部分保持不变,得到一个新图象.当这个新图象与x轴恰好只有两个公共点时,b的取值范围是______.
答案
(1)解法一:∵抛物线y=mx2+(m-3)x-3(m>0)与y轴交于点C,
∴C(0,-3),
∵抛物线与x轴交于A、B两点,OB=OC,
∴B(3,0)或B(-3,0),
∵点A在点B的左侧,m>0,
∴抛物线经过点B(3,0),
∴0=9m+3(m-3)-3,
∴m=1,
∴抛物线的解析式为y=x2-2x-3.
解法二:令y=0,∴mx2+(m-3)x-3=0.∴(x+1)(mx-3)=0.
∴x=-1,x=
,3 m
∵m>0,点A在点B的左侧,
∴A(-1,0),B(
,0),3 m
令x=0,可得y=-3,
∴C(0,-3),
∴OC=3,
∵OB=OC,
∴
=3,3 m
∴m=1,
∴y=x2-2x-3.
(2)①由抛物线y=x2-2x-3可知对称轴为x=1,
∵点P(x1,b)与点Q(x2,b)在这条抛物线上,且x1<x2,PQ=n,
∴x1=1-
,x2=1+n 2
,n 2
∴2x1=2-n,2x2=2+n,
∴原式=(2-n)2-(2+n)n+6n+3=7.
②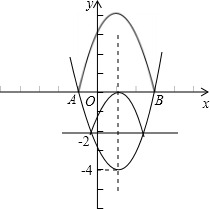
结合图形可得当这个新图象与x轴恰好只有两个公共点时,b的取值范围是:-4<b<-2或b=0.
