问题
解答题
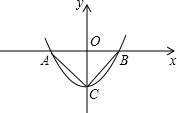
在直角坐标系xOy中,二次函数y=
∠ACB=90°,
(1)求点C的坐标及这个二次函数的解析式. (2)试设计两种方案:作一条与y轴不重合、与△ABC的两边相交的直线,使截得的三角形与△ABC相似,并且面积是△AOC面积的四分之一.求所截得的三角形三个顶点的坐标(说明:不要求证明). |
答案
(1)在y=
x2+1 2
nx+2-m中,令x=0,则y=2-m,3 4
则C的坐标是(0,2-m),则OC=m-2.
∵∠ACB=90°,
∴OC2=OA•OB,
设A、B的横坐标分别是x1,x2,则OA=-x1,OB=x2.
则x1•x2=
=4-2m,2-m 1 2
∴OC2=OA•OB=2m-4.
则(m-2)2=2m-4,解得:m=2(舍去)或4.
故m=4.则OC=4-2=2,
则C的坐标是(0,-2),
∵
+CO AO
=1,即BO CO
=CO2+AO•BO AO•CO
=2CO2 AO•CO
=1,2CO AO
∴AO=2CO=4,
则A的坐标是:(-4,0),
把(-4,0)以及m=4代入方程即可得到:8-3n-2=0,解得:n=2,
则二次函数的解析式是:y=
x2+1 2
x-2;3 2
(2)直角△OAC中,OA=OC=2,则当直线经过OA的中点,平行于OC时,使截得的三角形与△ABC相似,并且面积是△AOC面积的四分之一,则三个顶点的坐标是(-2,0)(-1,0),(-1,-1);
直角△OAC中,OA=OC=2,则当直线经过OA的中点,平行于OA时,使截得的三角形与△ABC相似,并且面积是△AOC面积的四分之一,则三个顶点的坐标是(0,-2),(0,-1),(-1,-1).