（1）∵拋物线与x轴交于点A（x₁，0）、B（x₂，0），

∴x₁、x₂是关于x的方程-

3

x2-2

3

(a-1)x-

3

(a2-2a)=0的解；

方程可化简为x²+2（a-1）x+（a²-2a）=0；

解方程，得x=-a或x=-a+2；

∵x₁＜x₂，-a＜-a+2，（1分）

∴x₁=-a，x₂=-a+2

∴A、B两点的坐标分别为A（-a，0），B（-a+2，0）（2分）

（2）∵AB=2，顶点C的纵坐标为

3

，（3分）

∴△ABC的面积等于

3

；（4分）

（3）∵x₁＜1＜x₂，

∴-a＜1＜-a+2

∴-1＜a＜1；（5分）

∵a是整数，

∴a=0，

即所求拋物线的解析式为y=-

3

x²+2

3

x；（6分）

解法一：此时顶点C的坐标为C（1，

3

）如图，作CD⊥AB于D，连接CQ，

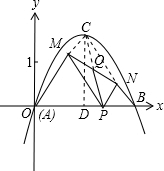则AD=1，CD=

3

，tan∠BAC=

3

，

∴∠BAC=60°

由拋物线的对称性可知△ABC是等边三角形；

由△APM和△BPN是等边三角形，线段MN的中点为Q可得，

点M、N分别在AC和BC边上，四边形PMCN的平行四边形，

C、Q、P三点共线，且PQ=

1

2

PC；（7分）

∵点P线段AB上运动的过程中，P与A、B两点不重合，

DC≤PC＜AC，DC=

3

，AC=2，

∴

3

2

≤PQ＜1；（8分）

解法二：设点P的坐标为P（x，0）（0＜x＜2）如图，作MM₁⊥AB于M₁，NN₁⊥AB于N₁

∵△APM和△BPN是等边三角形，且都在x轴上方，

∴AM=AP=x，BN=BP=2-x，∠MAP=60°，∠NBP=60°

∴AM₁=AM•cos∠MAB=

x

2

，

MM₁=AM•sin∠MAB=

3 x

2

，

BN₁=BN•cos∠NBP=

2-x

2

，

NN₁=BN•sin∠NBP=

2 3 - 3 x

2

∴AN₁=AB-BN₁=2-

2-x

2

=

2+x

2

∴M、N两点的坐标分）别为M（

x

2

，

3 x

2

），N（

2+x

2

，

2 3 - 3 x

2

）

可得线段MN的中点Q的坐标为Q（

x+1

2

，

3

2

）

由勾股定理得PQ=

(x- x+1 2 )2+( 3 2 )2

=

1

2

(x-1)2+3

（7分）

∵点P在线段AB上运动的过程中，P与A、B两点不重合，0＜x＜2，

∴3≤（x-1）²+3＜4，

∴

3

2

≤PQ＜1．（8分）