问题
解答题
已知函数f(x)=x3－3ax2＋2bx在点x=1处有极小值－1，试确定a,b的值，并求出f(x)的单调递增区间.
答案
在f(x)的单调递增区间为区间(－∞，－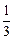
)和(1，＋∞)
由已知，可得f(1)=1－3a＋2b=－1. ①
又f′(x)=3x2－6a＋2b，
∴f′(1)=3－6a＋2b="0. " ② -------------------4分
由①②可得
故函数的解析式为f(x)=x3－x2－x. ----------------8分
由此得f′(x)=3x2－2x－1.
当f′(x)＞0时， x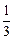＜－或x＞1。
因此在f(x)的单调递增区间为区间(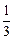－∞，－)和(1，＋∞).