问题
解答题
已知向量m＝(ex，ln x＋k)，n＝(1，f(x)]，m∥n(k为常数)，曲线y＝f(x)在点(1，f(1))处的切线与y轴垂直，F(x)＝xexf′(x)．
(1)求k的值及F(x)的单调区间；
(2)已知函数g(x)＝－x2＋2ax(a为正实数)，若对于任意x2∈[0,1]，总存在x1∈(0，＋∞)，使得g(x2)<F(x1)，求实数a的取值范围．
答案
（1）k＝1，F(x)的增区间为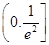
，减区间为
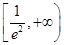.（2）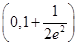
(1)由已知，得f(x)＝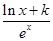
，∴f′(x)＝
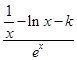，由已知，f′(1)＝
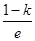＝0，∴k＝1，∴F(x)＝xexf′(x)＝x
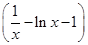＝1－xln x－x，所以F′(x)＝－ln x－2，由F′(x)＝－ln x－2≥0⇒0<x≤
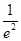，由F′(x)＝－ln x－2≤0⇒x≥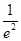∴F(x)的增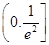区间为，减区间为.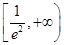
(2)∵对于任意x2∈[0,1]，总存在x1∈(0，＋∞)，
使得g(x2)<F(x1)，∴g(x)max<F(x)max .
由(1)知，当x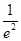＝时，F(x)取得最大值F
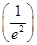＝1＋.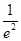
对于g(x)＝－x2＋2ax，其对称轴为x＝a，
当0<a≤1时，g(x)max＝g(a)＝a2，∴a2<1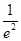＋，从而0<a≤1，当a>1时，g(x)max＝g(1)＝2a－1，∴2a－1<1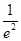＋，从而1<a<1＋
.
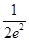综上可知：实数a的取值范围是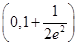.