问题
选择题
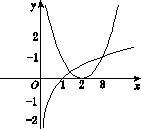
函数f(x)=ln x的图像与函数g(x)=x2-4x+4的图像的交点个数为( )
A.0
B.1
C.2
D.3
答案
答案:C
方法一,作出函数f(x)=ln x,g(x)=x2-4x+4的图像如图所示,则两个函数图像的交点个数为2,故选C.
方法二,构造函数φ(x)=ln x-x2+4x-4,则φ′(x)=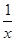 -2x+4=-
-2x+4=-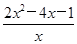 .又因为方程2x2-4x-1=0的大于零的根的是x0=
.又因为方程2x2-4x-1=0的大于零的根的是x0=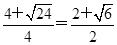 ,且在(0,x0)上φ′(x)>0,在(x0,+∞)上φ′(x)<0,所以函数φ(x)至多有两个零点.由于φ(1)=-1<0,φ(2)=ln 2>0,φ(4)=ln 4-4<0,则函数φ(x)有两个不同的零点.故函数f(x)=ln x的图像与函数g(x)=x2-4x+4的图像的交点个数为2.
,且在(0,x0)上φ′(x)>0,在(x0,+∞)上φ′(x)<0,所以函数φ(x)至多有两个零点.由于φ(1)=-1<0,φ(2)=ln 2>0,φ(4)=ln 4-4<0,则函数φ(x)有两个不同的零点.故函数f(x)=ln x的图像与函数g(x)=x2-4x+4的图像的交点个数为2.