问题
解答题
设f(x)=ax3+bx+c(a≠0)为奇函数,其图象在点(1,f(1))处的切线与直线x-6y-7=0垂直,导函数f′(x)的最小值为-12.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调增区间,并求函数f(x)在[-1,3]上的最大值和最小值.
答案
(1)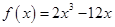 ;(2)
;(2)  、
、
题目分析:(1)根据 为奇函数可得
为奇函数可得 。由导数的几何意义可得
。由导数的几何意义可得 ,
, 的最小值可求
的最小值可求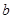 ,从而可得
,从而可得 的解析式。(2)先求导,在令导数大于0得增区间,令导数小于零得减区间,从而求得在
的解析式。(2)先求导,在令导数大于0得增区间,令导数小于零得减区间,从而求得在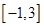 上的极值。再求两端点处函数值,比较极值与端点处函数值最小的为最小值,最大的为最大值。
上的极值。再求两端点处函数值,比较极值与端点处函数值最小的为最小值,最大的为最大值。
试题解析:
解:(1)∵ 为奇函数,∴
为奇函数,∴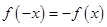 1分
1分
即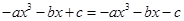 ,∴
,∴ . 2分
. 2分
又 的最小值为
的最小值为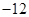 ,∴.
,∴.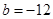 4分
4分
由题设知 ,∴
,∴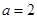 ,
,
故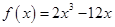 6分
6分
(2)  7分
7分
当 变化时,
变化时, 、
、 的变化情况表如下:
的变化情况表如下:

∴函数 的单调递增区间为
的单调递增区间为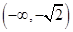 和
和 8分
8分
∵ ,极小值
,极小值 ,极大值
,极大值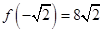 ,
,
当 时,
时,  ;当
;当 时,
时, . 10分
. 10分
