在平面直角坐标系中，横坐标与纵坐标都是整数的点（x，y）称为整

问题填空题

在平面直角坐标系中，横坐标与纵坐标都是整数的点（x，y）称为整点，如果将二次函数y=x²+8x-

的图象与x轴所围成的封闭图形染成红色，则此红色区域内部及其边界上的整点个数有______个．

答案

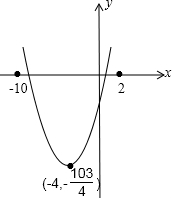
由二次函数y=x²+8x-

，得y=（x+4）²-

103

，

顶点为（-4，-

103

）．

令y=0，则x=-4-

103

≈-9.07或x=-4+

103

≈1.07，

故在红色区域内部及其边界上的整点有：

（-9，0），（-8，0），（-7，0），（-6，0），（-5，0），（-4，0），（-3，0），（-2，0），（-1，0），（0，0），（1，0），共11个；

（-8，-1），（-8，-2），…，（-8，-9），共9个；

（-7，-1），（-7，-2），…，（-7，-16），共16个；

（-6，-1），（-6，-2），…，（-6，-21），共21个；

（-5，-1），（-5，-2），…，（-5，-24），共24个；

（-4，-1），（-4，-2），…，（-4，-25），共25个；

由对称性，可知（-3，-1），（-3，-2），…，（-3，-24），共24个；

（-2，-1），（-2，-2），…，（-2，-21），共21个；

（-1，-1），（-1，-2），…，（-1，-16），共16个；

（0，-1），（0，-2），…，（0，-9），共9个；

一共11+2（9+16+21+24）+25=176个，

故答案为：176．