（1）f(x)的递增区间是(0，＋∞)，递减区间是(－1,0)．

（2）(2－2ln 2,3－2ln 3]．

题目分析：解　(1)函数的定义域为(－1，＋∞)，

因为f(x)＝(1＋x)²－2ln(1＋x)，

所以f′(x)＝2＝，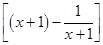

由f′(x)＞0，得x＞0；由f′(x)＜0，得－1＜x＜0，

所以，f(x)的递增区间是(0，＋∞)，递减区间是(－1,0)．

(2)方程f(x)＝x²＋x＋a，即x－a＋1－2ln(1＋x)＝0，

记g(x)＝x－a＋1－2ln(1＋x)(x＞－1)，

则g′(x)＝1－＝，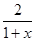

由g′(x)＞0，得x＞1；

由g′(x)＜0，得－1＜x＜1.

所以g(x)在[0,1]上单调递减，在[1,2]上单调递增．

为使f(x)＝x²＋x＋a在[0,2]上恰有两个相异的实根，

只须g(x)＝0在[0,1)和(1,2]上各有一个实根，

于是有即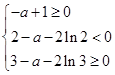

解得2－2ln 2＜a≤3－2ln 3，

故实数a的取值范围是(2－2ln 2,3－2ln 3]．

点评：解决的关键是根据导数判定函数单调性，以及函数的零点问题，属于中档题。