已知函数f(x)=ax+x2-xlna(a>0,a≠1).
(1)当a>1时,求证:函数f(x)在(0,+∞)上单调递增;
(2)若函数y=|f(x)-t|-1有三个零点,求t的值;
(3)若存在x1、x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1,试求a的取值范围.
(1)见解析(2)t=2(3)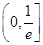 ∪[e,+∞)
∪[e,+∞)
审题引导:本题考查函数与导数的综合性质,函数模型并不复杂,(1)(2)两问是很常规的,考查利用导数证明单调性,考查函数与方程的零点问题.第(3)问要将“若存在x1、x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1”转化成|f(x)max-f(x)min|=f(x)max-f(x)min≥e-1成立,最后仍然是求值域问题,但在求值域过程中,问题设计比较巧妙,因为在过程中还要构造函数研究单调性来确定导函数的正负.
规范解答:(1)证明:f′(x)=axlna+2x-lna=2x+(ax-1)·lna.(2分)
由于a>1,故当x∈(0,+∞)时,lna>0,ax-1>0,所以f′(x)>0.
故函数f(x)在(0,+∞)上单调递增.(4分)
(2)解:当a>0,a≠1时,因为f′(0)=0,且f′(x)在R上单调递增,故f′(x)=0有唯一解x=0.(6分)所以x、f′(x)、f(x)的变化情况如下表所示:
| x | (-∞,0) | 0 | (0,+∞) |
| f′(x) | - | 0 | + |
| f(x) | | 极小值 | |
(3)解:因为存在x1、x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1,所以当x∈[-1,1]时,|f(x)max-f(x)min|=f(x)max-f(x)min≥e-1.(12分)
由(2)知,f(x)在[-1,0]上递减,在[0,1]上递增,所以当x∈[-1,1]时,f(x)min=f(0)=1,f(x)max=max{f(-1),f(1)}.
而f(1)-f(-1)=(a+1-lna)-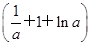 =a-
=a-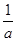 -2lna,
-2lna,
记g(t)=t- -2lnt(t>0),因为g′(t)=1+
-2lnt(t>0),因为g′(t)=1+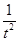 -
-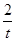 =
=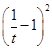 ≥0(当且仅当t=1时取等号),
≥0(当且仅当t=1时取等号),
所以g(t)=t- -2lnt在t∈(0,+∞)上单调递增,而g(1)=0,
-2lnt在t∈(0,+∞)上单调递增,而g(1)=0,
所以当t>1时,g(t)>0;当0<t<1时,g(t)<0,
也就是当a>1时,f(1)>f(-1);当0<a<1时,f(1)<f(-1).(14分)
①当a>1时,由f(1)-f(0)≥e-1a-lna≥e-1a≥e,
②当0<a<1时,由f(-1)-f(0)≥e-1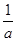 +lna≥e-10<a≤
+lna≥e-10<a≤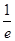 ,
,
综上知,所求a的取值范围为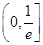 ∪[e,+∞).(16分)
∪[e,+∞).(16分)
