问题
解答题
若函数f(x)=ax3-x2+x-5在(-∞,+∞)上单调递增,求a的取值范围.
答案
a≥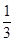
f′(x)=3ax2-2x+1,∵f(x)在(-∞,+∞)上单调递增,
∴f′(x)≥0即3ax2-2x+1≥0在R上恒成立.∴ ∴a≥
∴a≥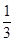 .
.
∴a的取值范围为a≥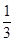 .
.
若函数f(x)=ax3-x2+x-5在(-∞,+∞)上单调递增,求a的取值范围.
a≥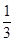
f′(x)=3ax2-2x+1,∵f(x)在(-∞,+∞)上单调递增,
∴f′(x)≥0即3ax2-2x+1≥0在R上恒成立.∴ ∴a≥
∴a≥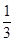 .
.
∴a的取值范围为a≥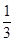 .
.