在平面直角坐标系xOy中，已知点A（-1，0），B（0，1），C（2，95

问题解答题

在平面直角坐标系xOy中，已知点A（-1，0），B（0，1），C（2，

）．
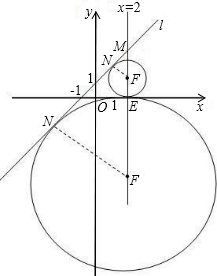
（Ⅰ）直线l：y=kx+b过A、B两点，求k、b的值；
（Ⅱ）求过A、B、C三点的抛物线Q的解析式；
（Ⅲ）设（Ⅱ）中的抛物线Q的对称轴与x轴相交于点E，那么在对称轴上是否存在点F，使⊙F与直线l和x轴同时相切？若存在，求出点F的坐标；若不存在，请说明理由．

答案

（Ⅰ）∵直线y=kx+b过A、B两点，

∴

-k+b=0

b=1

（1分）

解这个方程组，

得k=1，b=1．（2分）

（Ⅱ）设抛物线的解析式为y=ax²+bx+c，

则有：

a-b+c=0

c=1

4a+2b+c=

（3分）

解这个方程组，

得

a=-

c=1

∴抛物线的解析式为y=-

x²+

x+1．（4分）

（Ⅲ）存在⊙F与直线l和x轴同时相切．

易知抛物线Q的对称轴为x=2，（5分）

①当圆心F在x轴的上方时，

设点F的坐标为（2，y₀），把x=2代入y=x+1，

得y=3．

∴抛物线Q的对称轴与直线l的交点为M（2，3）．（6分）

∴EF=y₀，ME=3，MF=ME-EF=3-y₀．（7分）

由直线l：y=x+1知，

∠NMF=45度．

∴△MNF是等腰直角三角形

∴MF=

NF=

∴3-y₀=

y_{0
∴y₀=3
2
-3
∴点F的坐标为（2，3
2
-3）．（8分）
②当圆心F在x轴的下方时，设点F的坐标为（2，y₀），则MF=3-y₀，FE=-y₀．
由△MNF为等腰直角三角形，得3-y₀=
2
y₀，（9分）
∴y₀=-3-3
2
∴点F的坐标为（2，-3-3
2
）．（10分）}