问题
解答题
某会议室用5盏灯照明，每盏灯各使用灯泡一只，且型号相同。假定每盏灯能否正常照明只与灯泡的寿命有关，该型号的灯泡寿命为1年以上的概率为p1，寿命为2年以上的概率为p2；从使用之日起每满1年进行一次灯泡更换工作，只更换已坏的灯泡，平时不换，
（Ⅰ）在第一次灯泡更换工作中，求不需要换灯泡的概率和更换2只灯泡的概率；
（Ⅱ）在第二次灯泡更换工作中，对其中的某一盏灯来说，求该盏灯需要更换灯泡的概率；
（Ⅲ）当p1=0.8，p2=0.3时，求在第二次灯泡更换工作中，至少需要更换4只灯泡的概率（结果保留两个有效数字）。
答案
解：（Ⅰ）在第一次更换灯泡工作中，不需要换灯泡的概率为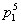
，
需要更换2只灯泡的概率为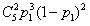
；
（Ⅱ）对该盏灯来说，在第1、2次都更换了灯泡的概率为（1-p1）2；
在第一次未更换灯泡而在第二次需要更换灯泡的概率为p1(1-p2)，
故所求的概率为
；
（Ⅲ）至少换4只灯泡包括换5只和换4只两种情况，换5只的概率为p5（其中p为（Ⅱ）中所求，下同），
换4只的概率为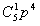
（1-p），
故至少换4只灯泡的概率为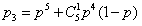
，
又当p1=0.8，p2=0.3时，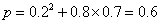
，
∴
，
即满两年至少需要换4只灯泡的概率为0.34。