问题
解答题
一条生产线上生产的产品按质量情况分为三类:A类、B类、C类。检验员定时从该生产线上任取2件产品进行一次抽检,若发现其中含有C类产品或2件都是B类产品,就需要调整设备,否则不需要调整。已知该生产线上生产的每件产品为A类品,B类品和C类品的概率分别为0.9,0.05和0.05,且各件产品的质量情况互不影响。
(Ⅰ)求在一次抽检后,设备不需要调整的概率;
(Ⅱ)若检验员一天抽检3次,以ξ表示一天中需要调整设备的次数,求ξ的分布列和数学期望。
答案
解:(Ⅰ)设Ai表示事件“在一次抽检中抽到的第i件产品为A类品”,i=1,2,
Bi表示事件“在一次抽检中抽到的第i件产品为B类品”, i=1,2,
C表示事件“一次抽检后,设备不需要调整”,
则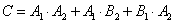 ,
,
由已知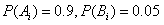 ,i=1,2,
,i=1,2,
所以,所求的概率为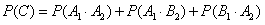
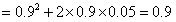 。
。
(Ⅱ)由(Ⅰ)知一次抽检后,设备需要调整的概率为 ,
,
依题意知,ξ的分布列为
ξ | 0 | 1 | 2 | 3 |
P | 0.729 | 0.243 | 0.027 | 0.001 |
 。
。 