问题
解答题
已知x＝3是函数f(x)＝aln(1＋x)＋x2－10x的一个极值点．
(1)求a；
(2)求函数f(x)的单调区间；
(3)若直线y＝b与函数y＝f(x)的图象有3个交点，求b的取值范围．
答案
（1）a＝16（2）单调增区间为(－1,1)，(3，＋∞)，单调减区间为(1,3)．（3）(32ln 2－21,16ln 2－9)
f(x)的定义域为(－1，＋∞)．
(1)f′(x)＝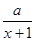
＋2x－10，又f′(3)＝
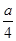＋6－10＝0，
∴a＝16.经检验此时x＝3为f(x)的极值点，故a＝16.
(2)由(1)知f′(x)＝
.
当－1<x<1或x>3时，f′(x)>0；
当1<x<3时，f′(x)<0.
∴f(x)的单调增区间为(－1,1)，(3，＋∞)，
单调减区间为(1,3)．
(3)由(2)知，f(x)在(－1,1)上单调递增，在(1,3)上单调递减，在(3，＋∞)上单调递增，且当x＝1或x＝3时，f′(x)＝0.所以f(x)的极大值为f(1)＝16ln 2－9，极小值为f(3)＝32ln 2－21.
因为f(16)>162－10×16>16ln 2－9＝f(1)，
f(e－2－1)<－32＋11＝－21<f(3)，
所以根据函数f(x)的大致图象可判断，在f(x)的三个单调区间(－1,1)，(1,3)，(3，＋∞)内，直线y＝b与y＝f(x)的图象各有一个交点，当且仅当f(3)<b<f(1)．
因此b的取值范围为(32ln 2－21,16ln 2－9)．