问题
选择题
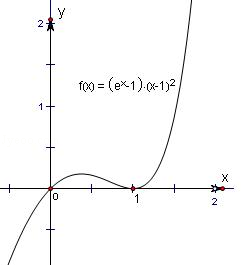
(2013•浙江)已知e为自然对数的底数,设函数f(x)=(ex﹣1)(x﹣1)k(k=1,2),则( )
A.当k=1时,f(x)在x=1处取得极小值
B.当k=1时,f(x)在x=1处取得极大值
C.当k=2时,f(x)在x=1处取得极小值
D.当k=2时,f(x)在x=1处取得极大值
答案
答案:C
当k=1时,函数f(x)=(ex﹣1)(x﹣1).
求导函数可得f'(x)=ex(x﹣1)+(ex﹣1)=(xex﹣1),
f'(1)=e﹣1≠0,f'(2)=2e2﹣1≠0,
则f(x)在在x=1处与在x=2处均取不到极值,
当k=2时,函数f(x)=(ex﹣1)(x﹣1)2.
求导函数可得f'(x)=ex(x﹣1)2+2(ex﹣1)(x﹣1)=(x﹣1)(xex+ex﹣2),
∴当x=1,f'(x)=0,且当x>1时,f'(x)>0,当x0<x<1时,f'(x)<0,故函数f(x)在(1,+∞)上是增函数;
在(x0,1)上是减函数,从而函数f(x)在x=1取得极小值.对照选项.
故选C.