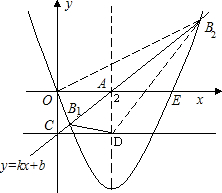
已知抛物线y=x2+bx+c经过原点,且在x轴的正半轴上截得的线段长为4,对称轴为直线x=m.过点A的直线绕点A(m,0)旋转,交抛物线于点B(x,y),交y轴负半轴于点C,过点C且平行于x轴的直线与直线x=m交于点D,设△AOB的面积为S1,△ABD的面积为S2.
(1)求这条抛物线的顶点的坐标;
(2)判断S1与S2的大小关系,并证明你的结论.
(1)∵抛物线y=x2+bx+c经过原点,且在x轴的正半轴上截得的线段的长为4,
∴c=0,A(2,0),图象与x轴的另一个交点E的坐标为(4,0),对称轴为直线x=2.
∴抛物线为y=x2+bx经过点E(4,0).
∴b=-4,∴y=x2-4x.
∴顶点坐标为(2,-4).
答:这条抛物线的顶点的坐标是(2,-4).
(2)答:S1与S2的大小关系是S1=S2.
证明:设经过点A(2,0)的直线为y=kx+b(k≠0),
∴0=2k+b.∴k=-
b,1 2
∴y=-
x+b,b 2
∴点B1的坐标为(x1,-
x+b),b 2
点B2的坐标为(x2,-
x+b),b 2
当交点为B1时,
S1=
×2×|-1 2
x1+b|=b-b 2
x1,b 2
S2=
×|b|×|2-x1|=b-1 2
x1,b 2
∴S1=S2,
当交点为B2时,
S1=
×2×|-1 2
x2+b|=-b 2
x2+b,b 2
S2=
×|b|×|x2-2|=-1 2
x2+b,b 2
∴S1=S2,
综上所述,S1=S2.