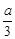(Ⅰ)a；(Ⅱ)m≤或m≥．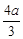

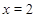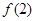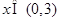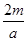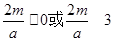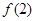题目分析：(Ⅰ) 求原函数的导函数，则导函数恒大于等于0，即可得所求；(Ⅱ)由(Ⅰ)知导函数时等于0，则为函数的极值，要使有最值，再看导函数为0时的另外一个根的范围，然后分情况讨论：①时，显然为最值；②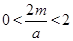时，先求(0，3)上的极值，然后再与端点函数值比较满足题意求m；③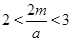时，先求(0，3)上的极值，然后再与端点函数值比较满足题意求m，综合①②③可得m的取值范围．

试题解析：(Ⅰ)由题意得f′(x)＝3ax²－6(m＋a)x＋12m＝3(x－2)(ax－2m)，

由于f(x)在(0，3)上无极值点，故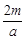＝2，所以m＝a．                         5分

(Ⅱ)由于f′(x)＝3(x－2)(ax－2m)，故

(i)当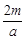≤0或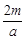≥3，即m≤0或m≥a时，

取x₀＝2即满足题意．此时m≤0或m≥a．

(ii)当0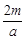＜＜2，即0＜m＜a时，列表如下:

x	0	(0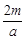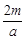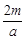，)		(，2)	2	(2，3)	3
f′(x)		＋	0	－	0	＋
f(x)	1	单调递增	极大值	单调递减	极小值	单调递增	9m＋1

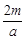故f(2)≤f(0)或f()≥f(3)，

即－4a＋12m＋1≤1或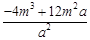＋1≥9m＋1，

即3m≤a或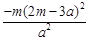≥0，

即m≤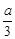或m≤0或m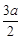＝．此时0＜m≤．

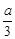(iii)当2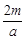＜＜3，即a＜m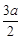＜时，列表如下:

x	0	(0，2)	2	(2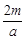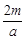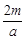，)		(，3)	3
f′(x)		＋	0	－	0	＋
f(x)	1	单调递增	极大值	单调递减	极小值	单调递增	9m＋1

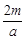故f()≤f(0)或f(2)≥f(3)，

即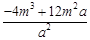＋1≤1或－4a＋12m＋1≥9m＋1，

即≤0或3m≥4a，

即m＝0或m≥3a或m≥．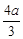

此时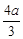≤m＜．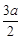

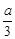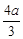综上所述,实数m的取值范围是m≤或m≥．               14分