问题
选择题
设f(x),g(x)分别是定义在R上的奇函数和偶函数.当x<0时,f′(x)g(x)+f(x)g′(x)> 0,且g(-3)=0,则不等式f(x)g(x)<0的解集是( )
A.(-3,0)∪(3,+∞)
B.(-3,0)∪(0,3)
C.(-∞,-3)∪(3,+∞)
D.(-∞,-3)∪(0,3)
答案
答案:D
题目分析:因为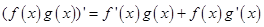 ,则由已知可得
,则由已知可得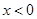 时,
时,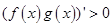 ,令
,令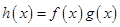 ,则函数
,则函数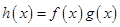 在
在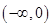 上单调递增。因为
上单调递增。因为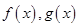 分别是在
分别是在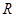 上的奇函数和偶函数,所以
上的奇函数和偶函数,所以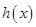 在
在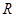 上是奇函数。则
上是奇函数。则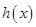 图像关于原点对称,且在
图像关于原点对称,且在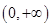 上也单调递增。因为
上也单调递增。因为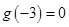 ,且
,且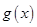 为偶函数则
为偶函数则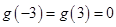 ,即
,即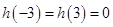 。综上可得
。综上可得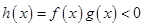 的解集为
的解集为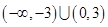 。故D正确。
。故D正确。
