(1) y=(a+1)x   (2) (-∞,-1]

(1)∵x>0,f'(x)=+a,

∴f'(1)=a+1,切点是(1,a+1),

所以切线方程为y-(a+1)=(a+1)(x-1),

即y=(a+1)x.

(2)方法一:∵x>0,f'(x)=.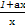

①当a≥0时,x∈(0,+∞),f'(x)>0,f(x)单调递增,显然当x>1时,f(x)>0,f(x)≤0不恒成立.

②当a<0时,x∈(0,-),f'(x)>0,f(x)单调递增,

x∈(-,+∞),f'(x)<0,f(x)单调递减,

∴f(x)_max=f(x)_极大值=f(-)=ln(-)≤0,

∴a≤-1,

所以不等式f(x)≤0恒成立时,a的取值范围是(-∞,-1].

方法二:∵x>0,所以不等式f(x)≤0恒成立,等价于ax≤-lnx-1,即a≤,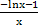

令h(x)=,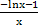

则h'(x)=-+=,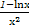

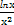当x∈(0,1)时,h'(x)<0,h(x)单调递减,

当x∈(1,+∞)时,h'(x)>0,h(x)单调递增.

∴h(x)_min=h(x)_极小值=h(1)=-1,∴a≤-1.

所以不等式f(x)≤0恒成立时,a的取值范围是(-∞,-1].