问题
解答题
已知函数f(x)=ax3+3x2-6ax-11,g(x)=3x2+6x+12和直线m:y=kx+9,且f′(-1)=0.
(1)求a的值.
(2)是否存在k的值,使直线m既是曲线y=f(x)的切线,又是曲线y=g(x)的切线?如果存在,求出k的值;如果不存在,说明理由.
答案
(1) a=-2 (2) 公切线是y=9,此时k=0
(1)f'(x)=3ax2+6x-6a,f'(-1)=0,
即3a-6-6a=0,∴a=-2.
(2)存在.∵直线m恒过定点(0,9),直线m是曲线y=g(x)的切线,设切点为(x0,3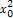
+6x0+12),
∵g'(x0)=6x0+6,
∴切线方程为y-(3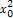+6x0+12)=(6x0+6)(x-x0),将点(0,9)代入,得x0=±1,
当x0=-1时,切线方程为y=9;
当x0=1时,切线方程为y=12x+9.
由f'(x)=0得-6x2+6x+12=0,
即有x=-1或x=2,
当x=-1时,y=f(x)的切线方程为y=-18;
当x=2时,y=f(x)的切线方程为y=9.
∴公切线是y=9.
又令f'(x)=12得-6x2+6x+12=12,
∴x=0或x=1.
当x=0时,y=f(x)的切线方程为y=12x-11;
当x=1时,y=f(x)的切线方程为y=12x-10,
∴公切线不是y=12x+9.
综上所述公切线是y=9,此时k=0.