问题
解答题
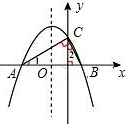
已知抛物线y=-
|
答案
∵图象与x轴有交点,∴令y=0,
∵图象与y轴有交点,∴令x=0,
∴y=n 即C点坐标为(0,n),
∵tan∠CAO=tan∠BCO=
,1 3
∴
=OC AO
=OB OC
,1 3
∵∠ACB=90°,CO⊥x轴,
∴OC2=AO•OB,
∵A、B两点在y轴异侧,
∴OA=3n,OB=
n,1 3
即n2=n,∵n≠0,∴n=1,∴OC=1,
∴AO=3,B0=1 3
∴A点坐标为(-3,0),
同理解得B点坐标为(
,0),1 3
设y=a(x+3)(x-
)1 3
且它过点C(0,1),
代入后解得:a=-1,
所以:y=-x2-
x-1.8 3
答:抛物线的解析式为:y=-x2-
x-1.8 3