(1) P(A·B)=P(A)·P(B)=0.6×0.6=0.36 (2)P(A·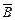)+P(·B)=0.24+0.24=0.48

(3)P=P(A·B)+［P(A·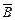)+P()·B］=0.36+0.48=0.84

(1)我们把“甲射击一次击中目标”叫做事件A，“乙射击一次击中目标”叫做事件B. 显然事件A、B相互独立，所以两人各射击一次都击中目标的概率是P(A·B)=P(A)·P(B)=0.6×0.6=0.36

答: 两人都击中目标的概率是0.36

(2)同理，两人各射击一次，甲击中、乙未击中的概率是

P(A·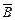)=P(A)·P(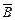)=0.6×(1－0.6)=0.6×0.4=0.24

甲未击中、乙击中的概率是P(·B)=P()P(B)=0.24，显然，“甲击中、乙未击中”和“甲未击中、乙击中”是不可能同时发生，即事件A·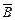与·B互斥，所以恰有一人击中目标的概率是

P(A·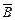)+P(·B)=0.24+0.24=0.48

答:其中恰有一人击中目标的概率是0.48.

(2)两人各射击一次，至少有一人击中目标的概率P=P(A·B)+［P(A·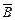)+P()·B］=0.36+0.48=0.84

答: 至少有一人击中目标的概率是0.84.