问题
填空题
设直线x＝t与函数f(x)＝x2，g(x)＝lnx的图象分别交于点M，N，则当|MN|达到最小时t的值为________．
答案
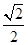
如图：|MN|＝f(t)－g(t)＝t2－lnt(t>0)，
令h(t)＝t2－lnt(t>0)，
则h′(t)＝2t－
＝
，
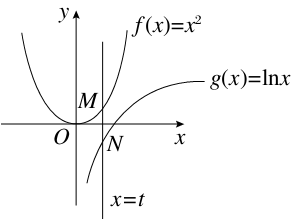
令h′(t)>0，得t>，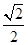
令h′(t)<0，得0<t<，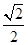
∴h(t)在(0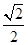，)上单调递减，在(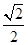，＋∞)上单调递增．
∴当t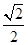＝时，h(t)取最小值，即t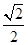＝时，|MN|取最小值．