问题
解答题
求过(-1,0),(3,0),(1,-5)三点的抛物线的解析式,并画出该抛物线.
答案
设抛物线的解析式为y=ax2+bx+c
将点(-1,0)(3,0)(1,-5)代入得
,a-b+c=0 9a+3b+c=0 a+b+c=-5
解得a= 5 4 b=- 5 2 c=- 15 4
所以抛物线的解析式为y=
x2-5 4
x-5 2 15 4
抛物线的图象如图所示:
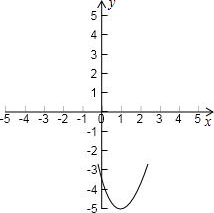
求过(-1,0),(3,0),(1,-5)三点的抛物线的解析式,并画出该抛物线.
设抛物线的解析式为y=ax2+bx+c
将点(-1,0)(3,0)(1,-5)代入得
,a-b+c=0 9a+3b+c=0 a+b+c=-5
解得a= 5 4 b=- 5 2 c=- 15 4
所以抛物线的解析式为y=
x2-5 4
x-5 2 15 4
抛物线的图象如图所示:
