（1）∵（OA+OB）²=OC²+16，

∴（-x₁+x₂）²=OC²+16，

∴4（k+

1

2

）²-4×2×（k+1）=（k+1）²+16，

解得k₁=-2，k₂=4．

∵x₁＜0＜x₂，

∴x₁•x₂=2（k+1）＜0，

即k＜-1，

∴k=-2．

∴抛物线解析式为y=

1

2

x²-

3

2

x-1

（2）过M、N、C三点的圆与直线CP只有一个公共点C．证明如下：

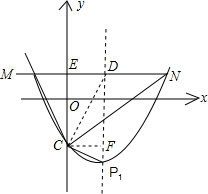
如图，∵抛物线上的点M、N在x轴上方，且到x轴距离均为1，设MN交y轴于E，

则M（-1，1），N（4，1），且C（0，-1），P（

3

2

，-

17

8

），

在Rt△MEC中，MC²=5，同理NC²=20，

又∵MN²=25，MN²-MC²=NC²，

∴∠MCN=90°．

故MN是过M、N、C三点的圆的直径，圆心D（

3

2

，1），

作CF⊥DP于F，连接CD，

则CFDE为矩形．

FD=CE=2，CF=ED=

3

2

，

又∵PF=

9

8

，

在Rt△CFP中，CP²=CF²+PF²=（

3

2

）²+（

9

8

）²=

225

64

，

在△CDP中，DP²-CD²=（

25

8

）²-（

5

2

）²=

225

64

=CP²，

即CP²+CD²=DP²，

∴CP⊥CD，直线CP与⊙D相切于点C，

故直线CP和过M、N、C三点的圆只有一个公共点C．