问题
解答题
已知抛物线y=x2+mx-2m2(m≠0).
(1)求证:该抛物线与x轴有两个不同的交点;
(2)过点P(0,n)作y轴的垂线交该抛物线于点A和点B(点A在点P的左边),是否存在实数m、n,使得AP=2PB?若存在,则求出m、n满足的条件;若不存在,请说明理由.
答案
(1)证明:△=m2-4×1×(-2m2)=9m2,
∵m≠0,∴△>0,
∴该抛物线与x轴有两个不同的交点;
(2)由题意易知:点A、B的坐标满足方程:x2+mx-2m2=n,即x2+mx-(2m2+n)=0
由于方程有两个不相等的实数根,
因此△>0,即m2-4×1×[-(2m2+n)]>0⇒9m2+4n>0,①
由求根公式可知两根为:xA=
,xB=-m- 9m2+4n 2
,-m+ 9m2+4n 2
∴AB=xB-xA=
--m+ 9m2+4n 2
=-m- 9m2+4n 2
,9m2+4n
PB=xB-xP=
-0=-m+ 9m2+4n 2
,-m+ 9m2+4n 2
分两种情况讨论:
第一种:如图1,点A在点P左边,点B在点P的右边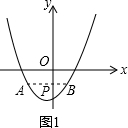
∵AP=2PB
∴AB=3PB
∴
=3×9m2+4n
⇒-m+ 9m2+4n 2
=3m.②9m2+4n
∴m>0.③
由②式可解得n=0.④
第二种:如图2,点A、B都在点P左边
∵AP=2PB
∴AB=PB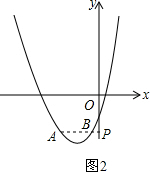
∴
=0-9m2+4n
⇒3-m+ 9m2+4n 2
=m.⑤9m2+4n
∴m>0.⑥
由⑤式可解得n=-
m2.⑦20 9
综合①③④⑥⑦可知,满足条件的点P存在,此时m、n应满足条件:m>0,n=0或n=-
m2.20 9
