问题
解答题
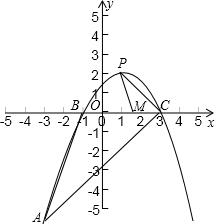
已知二次函数y=-
（1）求二次函数的解析式； （2）设点M为线段OC上一点，且∠MPC=∠BAC，求点M的坐标； 说明：若（2）你经历反复探索没有获得解题思路，请你在不改变点M的位置的情况下添加一个条件解答此题，此时（2）最高得分为3分． |
答案
把两点代入求解得：
-3b+c+
=0，3 2
b-c+
=0，1 2
解得：b=1，c=
，3 2
代入原函数解析式得：y=-
x2+x+1 2
．3 2
（2）如图所示：M点在OC上，
由题目可知∠MPC=∠BAC，点P的坐标为（1，2），
由已知个点坐标可以求得：CP=2
，AC=62
，BC=4，∠PCM=∠ACB=45°；2
由以上可以知道△PCM与△ACB相似，
所以有：
=PC CM
，AC BC
解得：CM=
，所以M点的坐标为（4 3
，0），5 3
答：M点的坐标为（
，0）．5 3
