问题
解答题
已知抛物线y=x2+1,求过点P(0,0)的曲线的切线方程.
答案
2x-y=0或2x+y=0.
设抛物线过点P的切线的切点为Q (x0,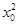 +1).
+1).
则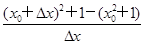 =Δx+2x0.
=Δx+2x0.
Δx→0时,Δx+2x0→2x0.
∴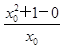 =2x0,∴x0=1或x0=-1.
=2x0,∴x0=1或x0=-1.
即切点为(1,2)或(-1,2).
所以,过P(0,0)的切线方程为y=2x或y=-2x.即2x-y=0或2x+y=0.
已知抛物线y=x2+1,求过点P(0,0)的曲线的切线方程.
2x-y=0或2x+y=0.
设抛物线过点P的切线的切点为Q (x0,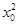 +1).
+1).
则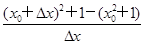 =Δx+2x0.
=Δx+2x0.
Δx→0时,Δx+2x0→2x0.
∴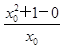 =2x0,∴x0=1或x0=-1.
=2x0,∴x0=1或x0=-1.
即切点为(1,2)或(-1,2).
所以,过P(0,0)的切线方程为y=2x或y=-2x.即2x-y=0或2x+y=0.