（1）由y=-

3

16

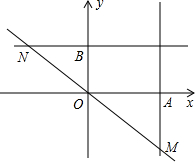
x²+3知：点A（4，0）、B（0，3）；

当x=4时，y=kx=4k，即：M（4，4k）；

当y=3时，kx=3，x=

3

k

，即：N（

3

k

，3）；

∴AM=4|k|、BN=

3

|k|

；

∴S_△OBN=

1

2

OB•BN=

1

2

•3•

3

|k|

=

9

2|k|

，S_△MAO=

1

2

•OA•AM=

1

2

•4•4|k|=8|k|；

∴

S△OBN

S△MAO

=

9 2|k|

8|k|

=

9

16k2

．

（2）由S_△OBN=

1

4

S_△MAO，得：

S△OBN

S△MAO

=

1

4

，即：

9

16k2

=

1

4

，解得：k=±

3

2

；

当k=

3

2

时，M（4，6）、N（2，3）；

设抛物线的解析式为：y=ax²+bx+c，有：

16a+4b+c=6 4a+2b+c=3 c=3

，解得：

a= 3 8 b=- 3 4 c=3

∴抛物线的解析式：y=

3

8

x²-

3

4

x+3；

当k=-

3

2

时，M（4，-6）、N（-2，3），同理可求得抛物线的解析式为：y=-

3

8

x²-

3

4

x+3；

综上，过点M、N、B的二次函数的解析式为：y=

3

8

x²-

3

4

x+3或y=-

3

8

x²-

3

4

x+3．