问题
解答题
已知函数f(x)=x3+(1-a)x2-a(a+2)x+b(a，b∈R)，
(Ⅰ)若函数f(x)的图象过原点，且在原点处的切线斜率是-3，求a，b的值；
(Ⅱ)若函数f(x)在区间（-1，1）上不单调，求a的取值范围。
答案
解：(Ⅰ)由函数f(x)的图象过原点得b=0，
又f′(x)=3x2+2(1-a)x-a(a+2)，
f(x)在原点处的切线斜率是-3，
则-a(a+2)=-3，所以a=-3或a=1．
(Ⅱ)由f′(x)=0，得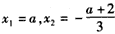
，
又f(x)在区间（-1，1）上不单调，即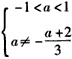
或
，
解得
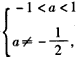或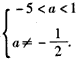
，
所以a的取值范围是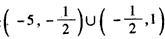
。