如果抛物线y=-x2+2(m-1)x+m+1与x轴都交于A,B两点,且A点在x轴的正半轴上,B点在x轴的负半轴上,OA的长是a,OB的长是b.
(1)求m的取值范围;
(2)若a:b=3:1,求m的值,并写出此时抛物线的解析式;
(3)设(2)中的抛物线与y轴交于点C,抛物线的顶点是M,问:抛物线上是否存在点P,使△PAB的面积等于△BCM面积的8倍?若存在,求出P点的坐标;若不存在,请说明理由.
(1)设A,B两点的坐标分别是(x1,0)、(x2,0),
∵A,B两点在原点的两侧,
∴x1x2<0,即-(m+1)<0,
解得m>-1.
∵△=[2(m-1)]2-4×(-1)×(m+1)
=4m2-4m+8
=4×(m-
)2+71 2
当m>-1时,△>0,
∴m的取值范围是m>-1;
(2)∵a:b=3:1,设a=3k,b=k(k>0),
则x1=3k,x2=-k,
∴
,3k-k=2(m-1) 3k•(-k)=-(m+1)
解得m1=2,m2=
.1 3
∵m=
时,x1+x2=-1 3
(不合题意,舍去),4 3
∴m=2,
∴抛物线的解析式是y=-x2+2x+3;
(3)易求抛物线y=-x2+2x+3与x轴的两个交点坐标是A(3,0),B(-1,0)
与y轴交点坐标是C(0,3),顶点坐标是M(1,4).
设直线BM的解析式为y=px+q,
则
.4=p•1+q 0=p•(-1)+q
解得
.p=2 q=2
∴直线BM的解析式是y=2x+2.
设直线BM与y轴交于N,则N点坐标是(0,2),
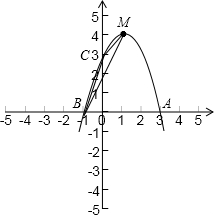
∴S△BCM=S△BCN+S△MNC
=
×1×1+1 2
×1×11 2
=1
设P点坐标是(x,y),
∵S△ABP=8S△BCM,
∴
×AB×|y|=8×1.1 2
即
×4×|y|=8.1 2
∴|y|=4.
∴y=±4.
当y=4时,P点与M点重合,即P(1,4),
当y=-4时,-4=-x2+2x+3,
解得x=1±2
.2
∴满足条件的P点存在.
P点坐标是(1,4),(1+2
,-4)(1-22
,-4).2
