问题
解答题
已知函数f(x)＝x2－1与函数g(x)＝aln x(a≠0)．
(1)若f(x)，g(x)的图像在点(1,0)处有公共的切线，求实数a的值；
(2)设F(x)＝f(x)－2g(x)，求函数F(x)的极值．
答案
（1）a＝2. （2）见解析
解：(1)因为f(1)＝0，g(1)＝0，
所以点(1,0)同时在函数f(x)，g(x)的图像上，
因为f(x)＝x2－1，g(x)＝aln x，
所以f′(x)＝2x，g′(x)＝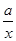
，
由已知，得f′(1)＝g′(1)，所以2＝
，即a＝2.
(2)因为F(x)＝f(x)－2g(x)＝x2－1－2aln x(x>0)，
所以F′(x)＝2x－
＝
，
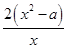当a<0时，
因为x>0，且x2－a>0，所以F′(x)>0对x>0恒成立，
所以F(x)在(0，＋∞)上单调递增，F(x)无极值；
当a>0时，
令F′(x)＝0，解得x1＝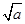
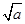，x2＝－ (舍去)，
所以当x>0时，F′(x)，F(x)的变化情况如下表：
| x | (0，) | | (，＋∞) |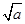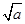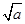
| F′(x) | － | 0 | ＋ |
| F(x) | 递减 | 极小值 | 递增 |
所以当x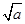＝时，F(x)取得极小值，且F(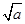)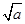＝()2－1－2aln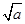＝a－1－aln a.
综上，当a<0时，函数F(x)在(0，＋∞)上无极值；
当a>0时，函数F(x)在x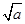＝处取得极小值a－1－aln a.