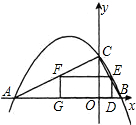问题
解答题
已知,二次函数y=mx2+3(m-
(1)求这个二次函数的解析式; (2)矩形DEFG的一条边DG在AB上,E、F分别在BC、AC上,设OD=x,矩形DEFG的面积为S,求S关于x的函数解析式; (3)将(1)中所得抛物线向左平移2个单位后,与x轴交于A′、B′两点(A′在B′的左边),矩形D′E′F′G′的一条边D′G′在A′B′上(G′在D′的左边),E′、F′分别在抛物线上,矩形D′E′F′G′的周长是否存在最大值?若存在,请求出最大值;若不存在,请说明理由. |
答案
(1)∵CO2=AO•OB
m=-1 4
y=-
x2-1 4
x+43 2
(2)A(-8,0),B(2,0)
OD=x
ED=4-2x,EF=5x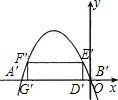
S=ED•EF=-10x2+20x(0<x<2)
(3)平移后的抛物线y′=-
x2-1 4 5 2
∴A′(-10,0)B′(0,0)
设D′(x,0),则G′(-10-x,0)
E′(x,-
x2-1 4
x),5 2
F′(-10-x,-
x2-1 4
x)5 2
C矩形D'E'F'G′=2(GD+DE)
=2[10+2x+(-
x2-1 4
x)]5 2
=-
x2-x+20(-5<x<0)1 2
当x=-1时,C矩形D′E′F′G′最大值=20.5.