问题
解答题
已知抛物线y=2x2+1。求
（1）抛物线上哪一点的切线的倾斜角为45°？
（2）抛物线上哪一点的切线平行于直线4x-y-2=0？
（3）抛物线上哪一点的切线垂直于直线x+8y-3=0？
答案
解：设点的坐标为（x0，y0），
则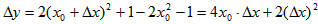
，
∴
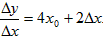
当△x无限趋近于零时，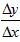
无限趋近于4x0，
即f′（x0）=4x0，
（1）∵抛物线的切线的倾斜角为45°，
∴斜率为tan45°=1，
即f′（x0）=4x0=1得
，该点为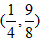
；
（2）∵抛物线的切线平行于直线4x-y-2=0，
∴斜率为4，
即f'（x0）=4x0=4得x0=1，
∴该点为（1，3）；
（3）∵抛物线的切线与直线x+8y-3=0垂直，
∴斜率为8，
即f′（x0）=4x0=8，得x0=2，
∴该点为（2，9）。
