问题
解答题
已知函数f(x)=(x-a)2(x-b)(a，b∈R，a＜b)，
(1)当a=1，b=2时，求曲线y=f(x)在点(2，f(2))处的切线方程；
(2)设x1，x2是f(x)的两个极值点，x3是f(x)的一个零点，且x3≠x1，x3≠x2，证明：存在实数x4，使得x1，x2，x3，x4按照某种顺序排列后构成等差数列，并求x4。
答案
解：(1)当a=1，b=2时，f(x)=(x-1)2(x-2)=x3-4x2+5x-2，
所以f′(x)=3x2-8x+5，
故f′(2)=1，
又f(2)=0，
所以曲线y=f(x)在点(2，0)处的切线方程为y=x-2．
(2)因为f′(x)=3(x-a)(x-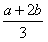
)，
由于a＜b，故a＜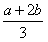
，
所以f(x)的两个极值点为x=a，x=，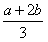
不妨设x1=a，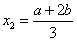
，
因为x3≠x1，x3≠x2，且x3是f(x)的一个零点，所以x3=b，
又因为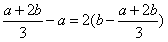
，
，
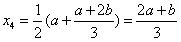所以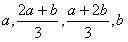
成等差数列，
所以存在实数x4满足题意，且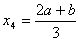
。