问题
解答题
甲设计了一个摸奖游戏，在一个口袋中装有同样大小的10个球，分别标有数字0，1，2，……9这十个数字，摸奖者交5元钱可参加一回摸球活动，一回摸球活动的规则是：摸奖者在摸球前先随机确定（预报）3个数字，然后开始在袋中不放回地摸3次球，每次摸一个，摸得3个球的数字与预先所报数字均不相同的奖1元，有1个数字相同的奖2元，2个数字相同的奖10元，3个数字相同的奖50元，设ξ为摸奖者一回所得奖金数，求ξ的分布列和摸奖人获利的数学期望.
答案
.
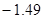题目分析：解：ξ为摸奖人摸一回所得奖金数，ξ可能取的值为1，2，10，50.
其中：P(ξ="1)="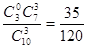 
； P(ξ="2)=" 
；
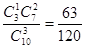P(ξ="10)="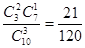 
； P(ξ="30)=" 
，
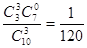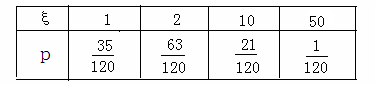
ξ的分布列：
∴Eξ=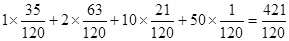
又设η为摸奖者获利的可能值，则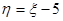
，
所以摸奖人获利的数学期望为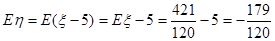
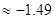
答：摸奖人获利的期望为.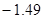
点评：解决的关键是利用组合数表示各个取值的概率值，然后借助于分布列得到期望，，属于基础题。