问题
解答题
设函数f(x)=ax+2，g(x)=a2x2-lnx+2，其中a∈R，x＞0，
(1)若a=2，求曲线y=g(x)在点(1，g(1))处的切线方程；
(2)是否存在负数a，使f(x)≤g(x)对一切正数x都成立？若存在，求出a的取值范围；若不存在，请说明理由．
答案
解：(1)由题意可知，当a=2时，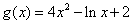
，
则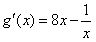
，
故曲线y=g(x)在点(1，g(1))处的切线斜率k=g'(1)=7，
又g(1)=6，
故曲线y=g(x)在点(1，g(1))处的切线方程为y-6=7(x-1)，即y=7x-1．
(2)设函数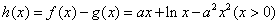
，
则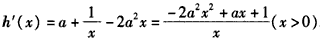
，
假设存在负数a，使得f(x)≤g(x)对一切正数x都成立，
即当x＞0时，h(x)的最大值小于等于零．
令h'(x)=0可得：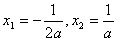
(舍)，
当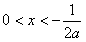
时，h'(x)＞0，h(x)单调递增；当
时，h'(x)＜0，h(x)单调递减，
即h(x)在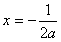
处有极大值，也是最大值，
所以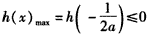
，解得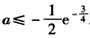
，
所以负数a存在，它的取值范围为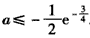
。