问题
解答题
用总长为32m的篱笆墙围成一个扇形的花园.
(1)试写出扇形花园的面积y(m2)与半径x(m)之间的函数关系式和自变量x的取值范围;
(2)用描点法作出函数的图象;
(3)当扇形花园半径为多少时,花园面积最大?最大面积是多少?此时这个扇形的圆心角是多大(精确到0.1度)?
(4)请回答:如果同样用32m的篱笆围成一个面积最大的矩形花园,这个花园的面积是多少?对比上面的结论,你有什么发现?
答案
(1)∵扇形半径为xm,
∴扇形的弧长为(32-2x)m.
由扇形面积公式得
y=
(32-2x)x,1 2
即y=-x2+16x.(3分)
自变量x的取值范围是0<x<16.(4分)
(2)将函数关系式写成y=-(x-8)2+64.
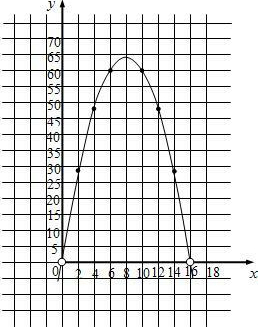
列表其图象如图所示:
| x | 2 | 4 | 6 | 8 | 10 | 12 | 14 |
| y | 28 | 48 | 60 | 64 | 60 | 48 | 28 |
即当扇形半径为8m时,花园面积最大,最大面积为64m2.
设此时扇形的圆心角约为n°,
则
•π•82=64解得n≈114.6°.n 360
因此,扇形的圆心角约为114.6°.(10分)
(4)这个矩形花园的面积也是64m2,与最大扇形花园面积相等(或答:周长相等的最大矩形面积与最大扇形的面积相等).(12分)