问题
解答题
已知函数f（x）=ax3+bx2+cx+d（a，b，c，d∈R），且函数f（x）的图象关于原点对称，其图象在x=3处的切线方程为8x-y-18=0。
（1）求f（x）的解析式；
（2）是否存在区间[m，n]，使得函数f（x）的定义域和值域均为[m，n]，且其解析式为f（x）的解析式？若存在，求出这样一个区间[m，n]；若不存在，则说明理由。
答案
解：（1）
的图象关于原点对称，
∴
恒成立，
即
，∴b=d=0，
又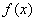
得图象在x=3处的切线方程为8x-y-18=0即
，
∴
，且
，
而
，∴
，
∴
，解得：
，
故所求函数的解析式为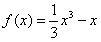
。
（2）解
。得x=0或
，
又
，
令
=0，得x=±1，
且当
或
时，
；
当x∈（-1，1）时，
<0，
∴
在
和
上递增，在[-1，1]上递减，
∴
在
上的极大值和极小值分别为
，
而
，
故存在这样的区间[m，n]，其中一个区间为
。