问题
解答题
已知函数f(x)＝x2－(1＋2a)x＋aln x(a为常数)．
(1)当a＝－1时，求曲线y＝f(x)在x＝1处切线的方程；
(2)当a>0时，讨论函数y＝f(x)在区间(0,1)上的单调性，并写出相应的单调区间．
答案
（1）y＝2x.
（2）函数f(x)的单调增区间是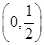
，单调减区间是
.
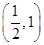解：(1)当a＝－1时，f(x)＝x2＋x－ln x，
则f′(x)＝2x＋1－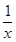
，
所以f(1)＝2，且f′(1)＝2.
所以曲线y＝f(x)在x＝1处的切线的方程为
y－2＝2(x－1)，即y＝2x.
(2)由题意得f′(x)＝2x－(1＋2a)＋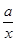
＝
＝
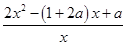
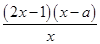(x>0)．
由f′(x)＝0，得x1＝
，x2＝a.
①当0<a<时，由f′(x)>0且x>0，
得0<x<a或<x<1；
由f′(x)<0且x>0，得a<x<.
所以函数f(x)的单调递增区间是(0，a)和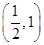，单调递减区间是
；
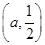②当a＝时，f′(x)＝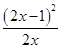
≥0，当且仅当x＝时，
f′(x)＝0.
所以函数f(x)在区间(0,1)上是单调递增函数；
③当<a<1时，由f′(x)>0且x>0，
得0<x<或a<x<1；
由f′(x)<0且x>0，得<x<a.
所以函数f(x)的单调递增区间是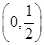和(a,1)，单调递减区间是
；
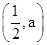④当a≥1时，由f′(x)>0且x>0，
得0<x<；
由f′(x)<0且x>0，得<x<1.
所以函数f(x)的单调增区间是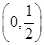，单调减区间是.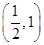