问题
解答题
设函数f(x)=x+ax2+blnx,曲线y=f(x)过P(1,0),且在P点处的切斜线率为2。
(1)求a,b的值;
(I2)证明:f(x)≤2x-2。
答案
解:(1)
由已知条件得 即
即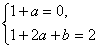
解得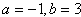 ;
;
(2)f(x)的定义域为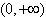
由(1)知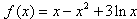
设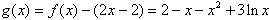
则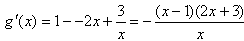
当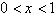 时,
时,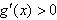
当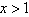 时,
时,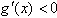
所以g(x)在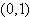 单调递增,在
单调递增,在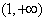 单调递减
单调递减
而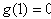
故当 时,
时,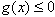 即
即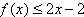 。
。
设函数f(x)=x+ax2+blnx,曲线y=f(x)过P(1,0),且在P点处的切斜线率为2。
(1)求a,b的值;
(I2)证明:f(x)≤2x-2。
解:(1)
由已知条件得 即
即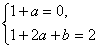
解得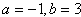 ;
;
(2)f(x)的定义域为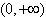
由(1)知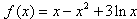
设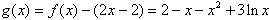
则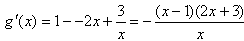
当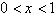 时,
时,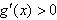
当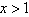 时,
时,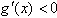
所以g(x)在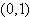 单调递增,在
单调递增,在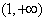 单调递减
单调递减
而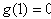
故当 时,
时,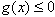 即
即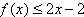 。
。