问题
解答题
（理）已知甲盒内有大小相同的3个红球和4个黑球，乙盒内有大小相同的5个红球和4个黑球．现从甲、乙两个盒内各任取2个球．
（1）求取出的4个球均为红球的概率；
（2）求取出的4个球中恰有1个红球的概率；
答案
（1）
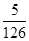；（2）
.
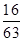第一问中，利用古典概型概率计算，设“从甲盒内取出的2个球均为红球”为事件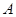
，“从乙盒内取出的2个球均为红球”为事件
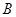．由于事件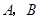
相互独立，且
， 
=
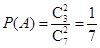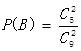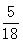故取出的4个球均为红球的概率是
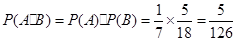
第二问中，利用解：设“从甲盒内取出的2个球中，1个是红球，1个是黑球；从乙盒内取出的2个均为黑球”为事件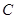
，“从甲盒内取出的2个球均为黑球；从乙盒内取出的2个球中，1个是红球，1个是黑球”为事件
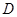．由于事件
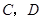互斥，且
，
．
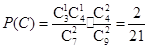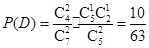故取出的4个红球中恰有1个红球的概率为
解：设“从甲盒内取出的2个球均为红球”为事件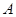，“从乙盒内取出的2个球均为红球”为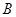事件．由于事件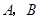相互独立，且
， =，
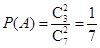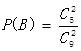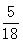故取出的4个球均为红球的概率是
．
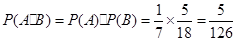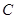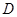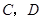（Ⅱ）解：设“从甲盒内取出的2个球中，1个是红球，1个是黑球；从乙盒内取出的2个均为黑球”为事件，“从甲盒内取出的2个球均为黑球；从乙盒内取出的2个球中，1个是红球，1个是黑球”为事件．由于事件互斥，且
，．
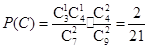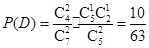故取出的4个红球中恰有4个红球的概率为
．
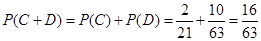