（1）∵y=ax²-4ax+4a+c=a（x-2）²+c，

∴抛物线的对称轴为直线x=2．

∵抛物线y=ax²-4ax+4a+c与x轴交于

点A、点B，点A的坐标为（1，0），

∴点B的坐标为（3，0），OB=3．

可得该抛物线的解析式为y=a（x-1）（x-3）．

∵OB=OC，抛物线与y轴的正半轴交于点C，

∴OC=3，点C的坐标为（0，3）．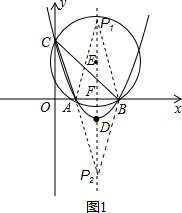

将点C的坐标代入该解析式，解得a=1．

∴此抛物线的解析式为：y=x²-4x+3；

（2）作△ABC的外接圆⊙E，设抛物线的对称轴与x轴的交点为点F，设⊙E与抛物线的对称轴位于x轴上方的部分的交点

为点P₁，点P₁关于x轴的对称点为点P₂，点P₁，点P₂，均为所求的点，如图1所示：

可知圆心E必在AB边的垂直平分线上即抛物线的对称轴直线x=2上，

∵∠AP₁B、∠ACB都是

AB

所对的圆周角，

∴∠AP₁B=∠ACB，且射线FE上的其它点P都不满足∠APB=∠ACB，

由（1）可知∠OBC=45°，AB=2，OF=2，

可得圆心E也在BC边的垂直平分线上即直线y=x上，

∴点E的坐标为：E（2，2），

由勾股定理可得出：EA=

5

，

∴EP₁=EA=

5

，

∴点P₁的坐标为：P₁（2，2+

5

），

由对称性得点P₂的坐标为：P₂（2，-2-

5

），

∴符合题意的点P坐标为：P₁（2，2+

5

），P₂（2，-2-

5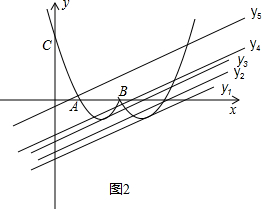

）；

（3）如图2，由题意可知，原二次函数的解析式为y=x²-4x+3可得，所求得的函数的解析式为：

y=(x-2)2-1(x＜3) y=(x-4)2-1(x≥3)

由函数图象可知：当y₁=

1

2

x+n与y=（x-4）²-1有一个交点时，

1

2

x+n=（x-4）²-1，

整理得出：x²-

17

2

x+15-n=0，

则b²-4ac=

289

4

-4（15-n）=0，

解得：n=-

49

16

，

∴当n＜-

49

16

时，动直线y=

1

2

x+n与函数图象无交点；

当n=-

49

16

时，动直线y=

1

2

x+n与函数图象有唯一的一个交点；

当y₁=

1

2

x+n与y=（x-2）²-1有一个交点时，

1

2

x+n=（x-2）²-1，

整理得出：x²-

9

2

x+3-n=0，

则b²-4ac=

81

4

-4（3-n）=0，

解得：n=-

33

16

，

∴当-

49

16

＜n＜-

33

16

时，动直线y=

1

2

x+n与函数图象有两个交点；

当n=-

33

16

时，动直线y=

1

2

x+n与函数图象有三个交点；

当y₁=

1

2

x+n过点B时，

1

2

×3+n=0，

解得：n=-

3

2

，

∴当-

33

16

＜n＜-

3

2

时，动直线y=

1

2

x+n与函数图象有四个交点；

当n=-

3

2

时，动直线y=

1

2

x+n与函数图象有三个交点；

当n＞-

3

2

时，动直线y=

1

2

x+n与函数图象有三个交点．