问题
解答题
附加题:已知二次函数y=ax2+bx+c的图象G和x轴有且只有一个交点A,与y轴的交点为B(0,4),且ac=b.
(1)求该二次函数的解析表达式;
(2)将一次函数y=-3x的图象作适当平移,使它经过点A,记所得的图象为L,图象L与G的另一个交点为C,求△ABC的面积.
答案
(1)由B(0,4)得,c=4.
G与x轴的交点A(-
,0),b 2a
由条件ac=b,得-
=-b 2a
=-2,c 2
即A(-2,0).
所以
.b=4a 4a-2b+4=0
解得
.a=1 b=4
所求二次函数的解析式为y=x2+4x+4.
(2)设图象L的函数解析式为y=-3x+b,
因图象L过点A(-2,0),
所以b=-6,
即平移后所得一次函数的解析式为
y=-3x-6.
令-3x-6=x2+4x+4,
解得x1=-2,x2=-5.
将它们分别代入y=-3x-6,
得y1=0,y2=9.
所以图象L与G的另一个交点为C(-5,9).
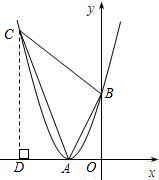
如图,过C作CD⊥x轴于D,
则S△ABC=S梯形BCDO-S△ACD-S△ABO
=
(4+9)×5-1 2
×3×9-1 2
×2×4=15.1 2